The sieve of Eratosthenes
One of the first algorithms any programmer interested in mathematics learns is the sieve of Eratosthenes. This is a simple algorithm that determines which numbers in a given range are prime, and it forms the basis of many more complex algorithmic problems.
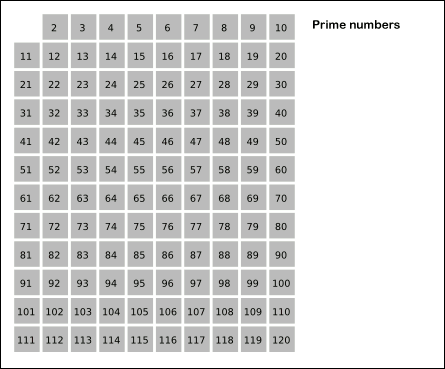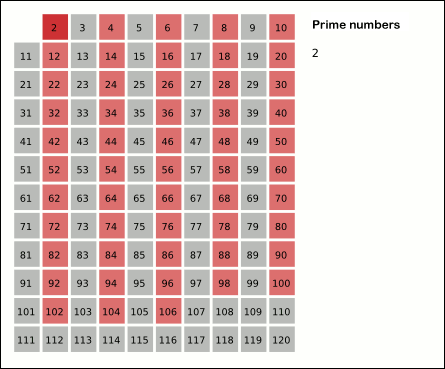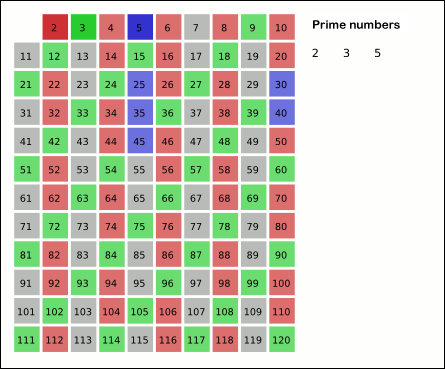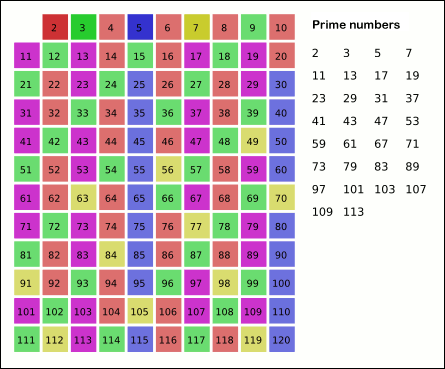
Given a list of consecutive integers starting from 2 up to a chosen maximum value n, the algorithm selects the first number in the list (2) and marks it as prime. It then marks all multiples of this number as non-prime. Next, it proceeds to the following unmarked number in the list, marks it as prime, and marks all of its multiples as non-prime. This process continues, moving to the following unmarked number and marking its multiples, until it reaches the square root of n, and the algorithm stops.
Primality testing is crucial to the field of cryptography, where large prime numbers are often generated for public-key encryption. The sieve of Eratosthenes is not used in complex cryptographic applications because more efficient algorithms are now available for probabilistically testing primality, such as the Miller-Rabin test. This standard method for generating prime numbers involves generating random values and using primality tests to determine whether they are prime or not.
However, the sieve remains a popular benchmark of computer performance due to its efficient time complexity: O(n log log n), and for its novelty. The earliest known reference to this algorithm dates back to the 2nd century CE, attributed to the ancient Greek polymath Eratosthenes of Cyrene.
Born in 276 BC in modern Libya, Eratosthenes was a mathematician, geographer (he coined the term), poet, astronomer, and music theorist. He was the chief librarian of the Library of Alexandria. There, he tutored Ptolemy IV and spent his free time copying books with such perfect quality that the library could not determine which book was the original and which was the duplicate. During his time in Alexandria, he devised a calendar based on the Earth's rotation. He calculated that every year consisted of 365 days, with every fourth year containing 366 days.
He also described and mapped the world, dividing the Earth into five climate zones with two freezing zones around the poles, two temperate zones, and a zone encompassing the equator and the tropics. Eratosthenes hypothesized that the Mediterranean had once been a vast lake, and that it only became connected to the ocean when a passage opened up at some point in its history. Evidence of this theory is found today through sediment deposits around the Mediterranean. Known as the Zanclean deluge theory, it is accepted as a possible cause of the formation of the Strait of Gibraltar.
Eratosthenes was also the first person to calculate the circumference of the Earth and the first to measure its axial tilt. He achieved this by measuring the angles of the sun with a rod in two different cities that he believed to be on the same meridian. The distance between the two cities was measured by bematists, specialists who were trained to measure distance by counting their steps. He divided the distance by the difference in the shadow angles, estimating a meridian length of 252,000 stadia. His estimation was correct to approximately −2.4% and +0.8%. This number is an approximation because the exact length of the ancient Greek unit of measurement he used, the stadion, is not known to us today.

Late in life, Eratosthenes contracted ophthalmia, swelling of the eyes, and he became blind. Without the ability to read, he voluntarily starved himself to death. When I get down and forget the point of what exactly I'm doing here, I like to remember him, and remember that behind every mathematical idea, there was once a curious mind reaching out into the unknown.